Ik heb een titel nodig die niets aan duidelijkheid te wensen overlaat. Bij dezen dus. Maar waarom eigenlijk? In een paar blogposts (niet achtereenvolgend, denk ik) ga ik een poging wagen enkele zaken uit te werken.
Goed, laat ik eerst de vraag rechtsreeks beantwoorden conform het huidige denken: we gaan als biologische wezens, rationele zoogdieren, allemaal dood.
Sorry, end of story.
Het 21ste eeuwse gedachtegoed rondom leven en sterven is kinderlijk eenvoudig. Het heeft de diepgang van een platbodem.
Dood is de norm; leven is de zeer zeldzame uitzondering.
Althans, dit is ons met de paplepel ingegoten; dit gedachtegoed rondom leven en sterven doordringt onze cultuur van de zolder tot de kelder.
Er zijn hier en daar wel pogingen onze dood toch ‘materieel’ zin te geven. Begraven worden bijvoorbeeld in een grafkist gemaakt van mycelium zodat het lijk sneller afbreekt tot voedingsstoffen.
Het dode lichaam als bron van biodiversiteit, te beginnen in de grond. Het is ‘zin geven aan een dood lichaam’. Okay. Snap ik ergens nog wel. Een heel klein beetje.
Maar het verandert de vraag eigenlijk ten diepste niet. Ben ik niets meer dan ‘voer voor wormen’ na mijn dood (schimmels in dit geval), of blijft er nog wat van mij over?
Als het eerste waar is, weet ik na mijn dood niets meer en doet alles er eigenlijk niets meer toe. Twee keer niets.
Mijn nabestaanden moeten een lijk opruimen, en dat kan op steeds meer manieren. Blijkbaar.
Maar stel dat er wél iets overblijft van mij, meer dan alleen chemicaliën voor het bodemleven, wat is dat dan, en hoe is dat in taal te verwoorden?
Laat ik eerst eerst eens een stap zijwaarts maken.
Veel wetenschappelijke en andere kennis van de werkelijkheid wordt niet zelden met veel aplomb gepresenteerd als ‘waar’.
Maar, wat is dat ook alweer, waarheid? Eerder zei ik er dit over:
“Er is geen waarheid zonder waarheidsmakers. Een ware bewering is gegrond in een feit/stand van zaken.
En, er zijn meerdere soorten waarheidsmakers, zoals ik opmerkte in dezelfde blogpost:
“Voor de MCU liefhebbers: dat Tony Stark de superheld Iron Man is, is een ware bewering. De bewering is waar omdat de bedenkers -Stan Lee, Larry Lieber en Don Heck- deze fictieve figuur als zodanig hebben verzonnen en niet omdat Tony Stark/Iron Man een echt persoon is die je op straat kunt ontmoeten!
Of wat te denken van de beroemde optelsom 2+2=4? De waarheidsmakers voor deze vergelijking vinden hun basis in de noodzakelijke verbanden tussen wiskundige concepten. Niet eenvoudig, dit soort wiskunde trouwens.
Zaken uit het verleden, zoals de aanslag op de nazi Reinhard Heydrich op 27 mei 1942 in Praag en zijn overlijden op 4 juni, hebben waarheidsmakers in getuigeverklaringen, documentatie, foto’s en dergelijke. De aanslag op en dood van Heydrich worden dus gestaafd door tal van verschillende waarheidsmakers.”
So far so good … hoop ik. Maar er ontbreekt iets fundamenteels aan deze kijk op waarheid.
Want: als ik dood ga, als iedereen dood gaat, blíjven deze zaken dan waar?
Anders gezegd: heeft waarheid eeuwigheidswaarde of heeft het een houdsbaarheidsdatum gekoppeld aan ons biologisch bestaan?
Laat ik deze kwestie verduidelijken: mijn eigen dood lijkt niets te veranderen aan het waarheidsgehalte van zaken in deze wereld.
Gelukkig maar. Zo belangrijk ben ik nou ook weer niet!
Maar: als de gehele mensheid verdwijnt kan niemand, van ons biologische soort althans, waarheden ontdekken, uitwerken, opschrijven, communiceren, enzovoort.
Nogmaals, als dát het geval is, blijven waarheden dan waarheden? Wat te denken, bijvoorbeeld, van de stelling van good ol’ Pythagoras:
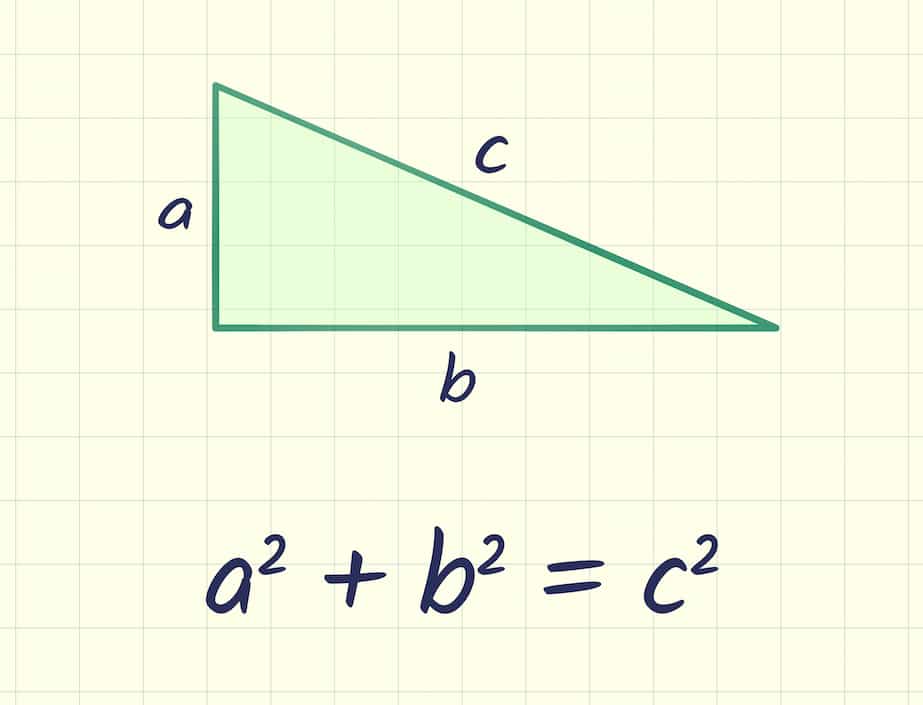
Verdwijnt deze wiskundige waarheid, of welk wiskundig bewijs dan ook, als wij allemaal zijn uitgestorven, of zelfs het gehele universum is verdwenen met al het andere eventuele intelligente leven?
(Ik kan natuurlijk beweren dat alle waarheden er dan niet meer toe doen. Áls dat al waar is: het nut van kennis stel ik hier niet aan de orde!)
Zien wij alles wat wij als waar omarmen als afspraken tussen mensen - ‘zo zijn onze manieren’ - of stijgen waarheden, zoals de stelling van Pythagoras, boven ons bestaan uit?
Laat ik deze kwestie op een andere manier benaderen. Nog een stapje zijwaarts: geduld geachte lezer.
Als kinderen leren tellen, dan ontdekken ze al heel snel dat je dóór kunt tellen. Van 1 naar 10 naar 20 naar 100. En dan komt de vraag als vanzelf: wat is het allergrootste getal?
Duizend is heel groot. Of honderdduizend. Of een miljoen. Een miljard misschien. Maar, aan dat ‘grootste getal’ kunt je altijd weer een volgend getal toevoegen: 1 miljard plus 1!
Kortom: de verzameling van alle natuurlijke getallen - 1, 2, 3, 4, 5, 6, 7, …, n - is oneindig groot. Je kunt blijven doortellen. En de meeste kinderen krijgen dat heel snel in de gaten.
En voor dat je het weet overtreft een natuurlijk getal de fysieke werkelijkheid van ons gehele universum.
Voorbeeld: een googol - 10^100 (10 tot de macht 100) - aan zandkorrels van ongeveer 0.5 mm in doorsnee kunnen het gehele universum vullen … maal 10 miljard.
Googol is trouwens nog maar een ‘klein getalletje’. Het kan nog veel, heel veel groter: Graham’s getal bijvoorbeeld.
Dit getal is een tijdlang recordhouder geweest als het grootste getal gebruikt in een wiskundig bewijs. (Bekijk deze video van Numberphile eens.)
Met natuurlijke getallen houdt het nooit op.

Zelfs dit soort uitzinnige getallen zijn nog altijd eindig en slechts een fractie van de oneindigheid van natuurlijke getallen.
Dit overtreft onze (gezamenlijke) mentale werkelijkheid.
Anders gezegd: alle ideeën en concepten die alle mensen (kunnen) weten of (kunnen) bedenken zijn beperkt en worden in omvang oneindig overstegen door de verzameling van alle natuurlijke getallen.
Hier stopt het overigens nog lang niet: de oneindigheid van natuurlijke getallen is nog maar ‘klein’ vergeleken met de veel grotere oneindigheden van de ‘overaftelbare’ getallen.
Natuurlijke getallen vormen een zogenaamde ‘aftelbare’ (oneindige) verzameling. Je kunt natuurlijke getallen ‘gewoon tellen’. Nou ja gewoon: dat tellen duurt dan wel oneindig lang.
Maar de verzameling van de reële getallen, tussen bijvoorbeeld 2 en 3, is niet te tellen. Letterlijk niet te tellen dus!
De decimale getallen die passen tussen deze twee naast elkaar liggende natuurlijke getallen zijn ontelbaar oneindig.
Ga maar na: we kunnen op weg naar 3 beginnen met 2.1, maar waarom niet met 2.01 of 2.001 of 2.0001 of 2.00000000001, en-zo-voort.
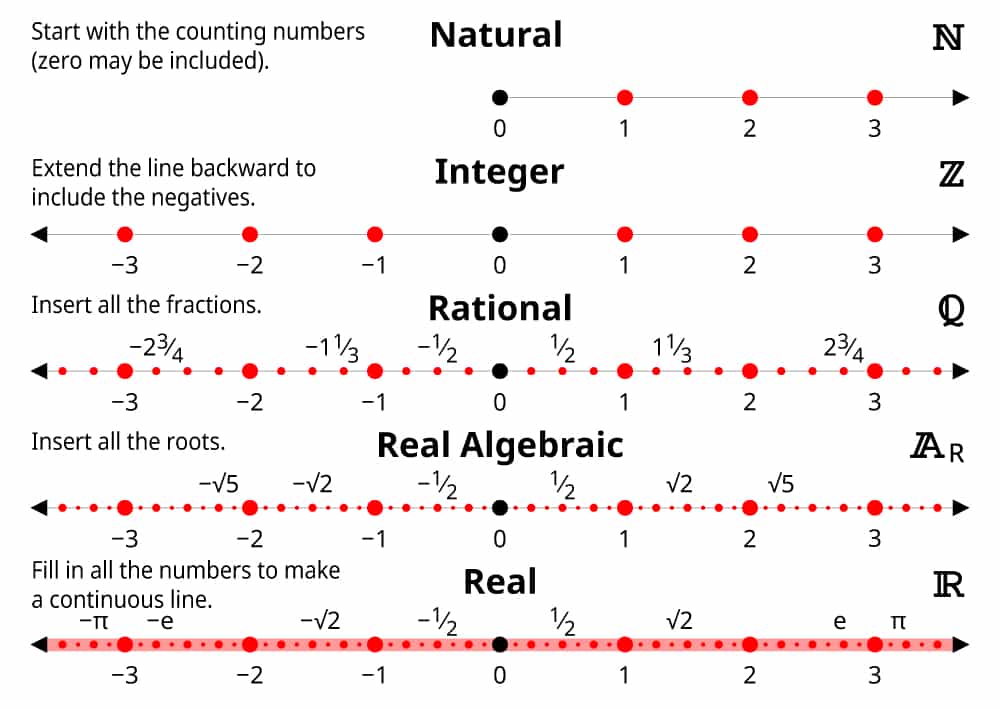
Voor de nerds (zoals uw, hopelijk gewaardeerde, blogger), bijgevoegd de opeenvolgende getallenverzamelingen van ‘kleine’ naar ‘grote’ oneindigheid.
Wat betekent dit geknutsel met oneindigheden allemaal?
In ieder geval dit: getallenverzamelingen zijn niet afhankelijk van alle materie in het gehele universum of zelfs de gecombineerde mentale capaciteit van alle mensen.
En dat moet verbazen en misschien zelfs wel angst inboezemen. En toch: we hebben oneindigheid heel hard nodig!
Een vreemde herinnering kan dit misschien illustreren. Als jong kind vreesde ik het moment dat astromen zouden aantonen dat het heelal waarin we leven eindig is wat betreft de omvang.
Ik stelde mij zo voor dat men met foto’s zou aankomen waarop een soort van muur zichtbaar zou zijn.
Zo van: kijk eens, díe muur. Dáár houdt het universum op.
Van die gedachte werd ik echt heel erg bang. Wij allemaal opgesloten in een hele grote kist met de stikker ‘heelal’ erop. Dat benauwde mij enorm, alsof ik al niet astmatisch genoeg was.
En toch zegt ons werk in de wiskunde, bijvoorbeeld, dat zelfs ons universum, hoe groot ook, ons niet in toom kan houden, ons niet kan beperken.
Hoewel ons heelal waarschijnlijk eindig is, zonder dat we dat ooit kunnen waarnemen trouwens, ‘spelen’, werken we met oneindigheid, hoewel we dat ten diepste niet kunnen bevatten.
Preciezer gezegd: oneindigheid omvat ons.
Precies deze notie geeft ons alle aanleiding om te vermoeden dat waarheid, die we ontdekken over onze werkelijkheid, geen houdbaarheidsdatum heeft.
Kortom: waarheid is eeuwig.
Waar dat toe leidt zullen we moeten zien. Op naar de volgende blogpost ….
